Video: Quale rotazione mapperà un esagono regolare su se stesso?
2024 Autore: Miles Stephen | [email protected]. Ultima modifica: 2023-12-15 23:37
Ci sono 6 angoli tra i vertici vicini, sono tutti uguali (perché a l'esagono è regolare ) e la loro somma è 360°. Quindi ogni angolo ha una misura di 360°/6=60°. Ogni successivo rotazione anche di 60° mappe un esagono su se stesso.
Allo stesso modo, quale rotazione mapperà un Nonagon su se stesso?
Per un normale nonagone , esso mappa su se stesso 9 volte durante a rotazione di 360°. Una forma è detto di avere rotazionale simmetria se mappa su se stesso sotto rotazione circa un punto al suo centro. L'ordine di rotazionale simmetria è il numero di volte la forma mappa su se stesso durante un rotazione di 360°.
Sapete anche, quali rotazioni, se ce ne sono, mappano la figura su se stessa? Una figura in aereo ha rotazionale simmetria Se il figura può essere mappato su se stesso di una rotazione tra 0° e 360° rispetto al centro di il figura . Non c'è modo per ruotare questo figura e averlo mappa su se stesso . Quindi, non ha rotazionale simmetria.
Di conseguenza, quale rotazione porterà su se stesso un Pentagono?
Questo perché il pentagono regolare ha simmetria di rotazione e egin{align*}72^circend{align*} è il numero minimo di gradi puoi ruotare il pentagono per portarlo su se stesso.
Qual è il minor numero di gradi necessari per ruotare su se stesso un esagono regolare?
Una rotazione ha 360 gradi. Poiché il Pentagono regolare ha 5 lati e ognuno di essi prende 360/5 = 72 gradi se visto dal centro, se ruotiamo il Pentagono regolare di 72 gradi otterremo la stessa forma da cui siamo partiti. Quindi la risposta è 72 gradi.
Consigliato:
Quale non metallo appartiene allo stesso gruppo del piombo?
Calcio. Quale non metallo appartiene allo stesso gruppo del piombo? Carbonio
Qual è la formula per calcolare la rotazione specifica dalla rotazione osservata?
Per convertire una rotazione osservata in una rotazione specifica, dividere la rotazione osservata per la concentrazione in g/mL e la lunghezza del percorso in decimetri (dm)
La rotazione ottica e la rotazione specifica sono le stesse?
In chimica, la rotazione specifica ([α]) è una proprietà di un composto chimico chirale. Se un composto è in grado di ruotare il piano di polarizzazione della luce polarizzata in piano, si dice che è "otticamente attivo". La rotazione specifica è una proprietà intensiva, che la distingue dal fenomeno più generale della rotazione ottica
È più probabile che elementi con proprietà chimiche simili si trovino nello stesso periodo o nello stesso gruppo spiega la tua risposta?
Questo perché le proprietà chimiche non dipendono da nessun elettrone di valenza. Come in un gruppo tutti gli elementi hanno lo stesso no dell'elettrone di valenza ecco perché hanno proprietà chimiche simili ma in un periodo il no dell'elettrone di valenza varia ecco perché differiscono nelle proprietà chimiche
Quale dei quadrilateri è un quadrilatero regolare?
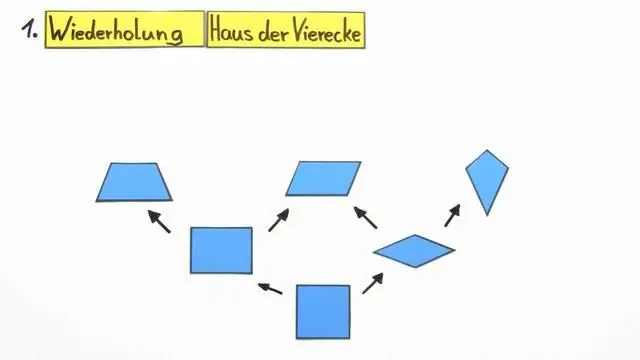
quadrato Inoltre chiesto, qual è la misura di un quadrilatero regolare? Sì, l'interno angoli di ogni angolo di un quadrilatero regolare sono ciascuno 90 gradi (360 gradi / 4 angoli). L'esterno angoli sono semplici da determinare; sottrai l'angolo interno dall'intero cerchio di 360 (360 - 90) e ottieni: