Sommario:
Video: Come si rappresentano le disuguaglianze su un piano di coordinate?
2024 Autore: Miles Stephen | [email protected]. Ultima modifica: 2023-12-15 23:37
Ci sono tre passaggi:
- Riorganizza l'equazione in modo che "y" sia a sinistra e tutto il resto a destra.
- Traccia la linea "y=" (rendila una linea continua per y≤ o y≥ e una linea tratteggiata per y)
- Ombreggia sopra la linea per un "maggiore di" (y> o y≥) o sotto la linea per un "minore di" (y< o y≤).
Allo stesso modo, viene chiesto, qual è lo scopo di ombreggiare una disuguaglianza quando si traccia un grafico su un piano di coordinate?
Quando sei rappresentazione grafica delle disuguaglianze , desideri grafico le normali funzioni lineari proprio come abbiamo fatto prima. La differenza è che la soluzione al disuguaglianza non è la linea tracciata ma l'area del piano di coordinate che soddisfa il disuguaglianza.
Sappi anche, come trovi la disuguaglianza? Queste cose non influenzano la direzione della disuguaglianza:
- Aggiungi (o sottrai) un numero da entrambi i lati.
- Moltiplica (o dividi) entrambi i membri per un numero positivo.
- Semplificare un lato.
Allo stesso modo, come si rappresentano le disuguaglianze su una retta numerica?
Basta seguire questi passaggi
- Trova il numero dall'altra parte del segno di disuguaglianza dalla variabile (come il 4 in x > 4).
- Disegna una linea numerica e disegna un cerchio aperto attorno a quel numero.
- Completa il cerchio se e solo se la variabile può anche essere uguale a quel numero.
- Ombreggia tutti i numeri che la variabile può essere.
Qual è la definizione di soluzione di un'equazione?
UN soluzione è un'assegnazione di espressioni alle variabili incognite che rende l'uguaglianza nel equazione vero. In altre parole, a soluzione è un'espressione o un insieme di espressioni (una per ogni incognita) tale che, quando sostituita alle incognite, la equazione diventa identità.
Consigliato:
Come si trova il fattore di scala di una dilatazione su un piano di coordinate?
Disegna il triangolo ABC con le coordinate A(2, 6), B(2, 2), C(6, 2). Quindi dilatare l'immagine di un fattore di scala di 1/2 con l'origine come centro di dilatazione. Per prima cosa, tracciamo il nostro triangolo originale nel piano delle coordinate. Successivamente, moltiplichiamo ciascuna coordinata per il fattore di scala di 1/2
Cosa sono le coordinate nel piano cartesiano?
Coordinate cartesiane del piano L'origine è l'intersezione degli assi x e y. Le coordinate cartesiane di un punto nel piano si scrivono come (x,y). La coordinata x specifica la distanza a destra (se x è positiva) oa sinistra (se x è negativa) dell'asse y
Quale prova usa le figure su un piano di coordinate per dimostrare le proprietà geometriche?
Una dimostrazione che utilizza figure su un piano di coordinate per dimostrare le proprietà geometriche è detta trigonometrica
Come si costruisce un piano di coordinate in geometria?
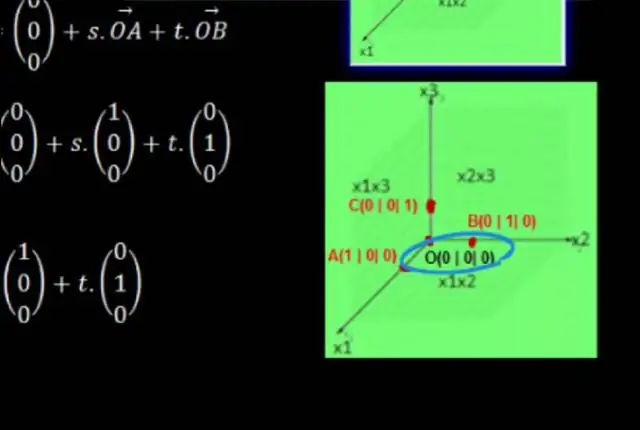
Per creare un piano di coordinate, seguiamo questi passaggi: Disegna due linee numeriche perpendicolari l'una all'altra, che si intersecano nel punto 0 su entrambe le linee. Etichetta la linea dei numeri orizzontale come l'asse x ed etichetta la linea dei numeri verticale come l'asse y
Cosa sono i numeri interi e razionali Come vengono rappresentati i punti su un piano di coordinate?
Come abbiamo detto, i punti sul piano delle coordinate sono rappresentati come (a, b), dove aeb sono numeri razionali. I numeri razionali sono numeri che possono essere scritti come una frazione, p/q, dove p e q sono numeri interi. Chiamiamo a la coordinata x del punto e chiamiamo b la coordinata y del punto