
- Autore Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- Ultima modifica 2025-06-01 05:04.
Piccolo teorema di Fermat afferma che se p è un numero primo, allora per ogni intero a, il numero a P - a è un multiplo intero di p. unP a (mod p). Caso speciale: se a non è divisibile per p, Piccolo teorema di Fermat è equivalente all'affermazione che a P-1-1 è un multiplo intero di p.
In questo modo, come si dimostra il piccolo teorema di Fermat?
Sia p un numero primo e un qualsiasi intero, quindi aP = a (mod p). Prova. Il risultato è trival (entrambi i lati sono zero) se p divide a. Se p non divide a, allora dobbiamo solo moltiplicare la congruenza in Piccolo teorema di Fermat da a per completare la dimostrazione.
Sappi anche, qual è la soluzione dell'ultimo teorema di Fermat? Soluzione per L'ultimo teorema di Fermat . L'ultimo teorema di Fermat (FLT), (1637), afferma che se n è un intero maggiore di 2, allora è impossibile trovare tre numeri naturali x, yez dove tale uguaglianza è soddisfatta essendo (x, y)>0 in xn+yn =zn.
Considerando questo, perché il piccolo teorema di Fermat è importante?
Piccolo teorema di Fermat è un fondamentale teorema nella teoria elementare dei numeri, che aiuta a calcolare le potenze degli interi modulo i numeri primi. È un caso speciale di Eulero teorema , ed è importante nelle applicazioni della teoria dei numeri elementare, compresi i test di primalità e la crittografia a chiave pubblica.
Cosa si intende per teorema di Eulero?
Teorema di Eulero . La generalizzazione di Fermat's teorema è conosciuto come il teorema di Eulero . Generalmente, il teorema di Eulero afferma che, "se p e q sono primi tra loro, allora ", dove è di Eulero funzione totient per numeri interi. Cioè, è il numero di numeri non negativi che sono minori di q e relativamente primi rispetto a q.
Consigliato:
Come si esegue il test di Durbin Watson in Minitab?
In Minitab: fare clic su Statistiche > Regressione > Regressione > Adatta modello di regressione. Fai clic su "Risultati" e controlla la statistica Durbin-Watson
Come si chiama un piccolo vulcano?

I coni di cenere sono il tipo più semplice di vulcano. Sono costituiti da particelle e blob di lava congelata espulsi da una singola bocca. Quando la lava carica di gas viene soffiata violentemente nell'aria, si rompe in piccoli frammenti che si solidificano e cadono come cenere intorno allo sfiato per formare un cono circolare o ovale
Come si esegue un cavo da un generatore in Fallout 4?

Basta costruire un piccolo generatore, quindi un oggetto che ha bisogno di energia (come la cosa dell'emittente dei coloni). Cammina verso il generatore e dovresti vedere un'opzione in basso per far passare un filo. Premi X per avviare il cavo al generatore, avvicinati all'oggetto alimentato, premi X e il cavo si completerà automaticamente. Voilà, potere
Come si esegue la regressione sinusoidale su una calcolatrice?
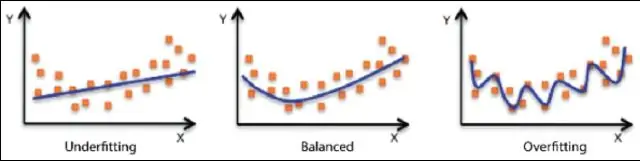
VIDEO Quindi, come si calcola la regressione sinusoidale? Regressione sinusoidale . Regola i valori di A, B, C e D in equazione y = A*sin(B(x-C))+D per fare a sinusoidale curva adatta a un dato insieme di dati generati casualmente.
Come si può spegnere più facilmente un piccolo incendio?

Sicurezza antincendio: estinguere piccoli incendi in un contenitore coprendo e tagliando l'ossigeno con un mascherino ceramico solido. Se i capelli o i vestiti di qualcuno prendono fuoco, cerca immediatamente di soffocare le fiamme con una coperta di lana o indumenti di cotone
