- Autore Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- Ultima modifica 2025-06-01 05:04.
Nelle statistiche, il 68 - 95 - 99,7 regola , noto anche come empirico regola , è una scorciatoia Usato ricordare la percentuale di valori che si trovano all'interno di una banda attorno alla media in una distribuzione normale con un'ampiezza rispettivamente di due, quattro e sei deviazioni standard; più precisamente, 68,27%, 95,45% e 99,73% dei valori giacciono
A questo proposito, qual è la regola del 95%?
L'empirico regola afferma che per una distribuzione normale, quasi tutti i dati rientreranno in tre deviazioni standard della media. 95 % rientra in due deviazioni standard. Il 99,7% rientra in tre deviazioni standard.
Inoltre, quali sono gli intervalli di confidenza del 68% 95% e 99,7% per le medie del campione? Da quando 95 La % dei valori rientra in due deviazioni standard del Significare secondo il 68 - 95 - 99.7 Regola, è sufficiente aggiungere e sottrarre due deviazioni standard da Significare per ottenere il 95 % intervallo di confidenza . Secondo il 68 - 95 - 99.7 Regola: ➢ Il 68 % intervallo di confidenza per questo esempio è compreso tra 78 e 82.
Anche sapere è, perché la deviazione standard è del 68 percento?
Come altri hanno detto, è un risultato del calcolo che questa formula calcolata come un integrale da -1/2 sigma a 1/2 sigma (che copre 1 sigma = 1 deviazione standard ) risulta in un'area sotto la curva di 0,68, con l'intera area, calcolata come integrale da -infinito a +infinito essendo 1, quindi ottieni 68 % per uno standard
Qual è l'intervallo di confidenza del 95%?
UN 95 % intervallo di confidenza è un intervallo di valori che puoi essere 95 % certa contiene la vera media della popolazione. Con il piccolo campione a sinistra, il 95 % intervallo di confidenza è simile alla gamma dei dati.
Consigliato:
Come si usa la regola del prodotto e del quoziente?

La regola del prodotto dice che la derivata di un prodotto di due funzioni è la prima funzione per la derivata della seconda funzione più la seconda funzione per la derivata della prima funzione. La regola del prodotto deve essere utilizzata quando si deve fare la derivata del quoziente di due funzioni
Qual è la differenza tra regola del prodotto e regola della catena?

Usiamo la regola della catena per differenziare una "funzione di una funzione", come f(g(x)) in generale. Usiamo la regola del prodotto per differenziare due funzioni moltiplicate insieme, come f(x)g(x) in generale. Ma nota che sono funzioni separate: una non si basa sulla risposta dell'altra
Come si usa la regola della mano destra per il prodotto incrociato?
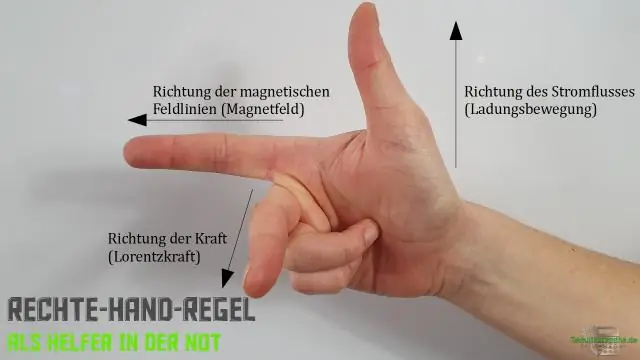
La regola della mano destra afferma che l'orientamento del prodotto vettoriale dei vettori è determinato posizionando e coda a coda, appiattendo la mano destra, estendendola nella direzione di, e quindi arricciando le dita nella direzione con cui forma l'angolo. Il pollice quindi punta nella direzione di
Come si converte la regola del quoziente in regola del prodotto?

La regola del quoziente potrebbe essere vista come un'applicazione delle regole del prodotto e della catena. Se Q(x) = f(x)/g(x), allora Q(x) = f(x) * 1/(g(x)). È possibile utilizzare la regola del prodotto per differenziare Q(x) e 1/(g(x)) può essere differenziato utilizzando la regola della catena con u = g(x) e 1/(g(x)) = 1/u
Puoi usare la regola del prodotto invece della regola del quoziente?

Ci sono due ragioni per cui la regola del quoziente può essere superiore alla regola della potenza più la regola del prodotto nel differenziare un quoziente: Conserva i denominatori comuni quando si semplifica il risultato. Se usi la regola della potenza più la regola del prodotto, spesso devi trovare un denominatore comune per semplificare il risultato
